
Effektives Einkaufsmanagement stellt eine große Herausforderung für viele Unternehmen dar. In SAP R/3 werden hier Möglichkeiten geboten, die Prognoseprozesse strukturiert durchzuführen und es empfiehlt sich dabei, die Einführung in sechs Phasen zu unterteilen.
1) Korrektur der Vergangenheitsdaten
Eine gute Prognose steht und fällt mit der Qualität der Vergangenheitswerte. Für die Korrektur der Vergangenheitsdaten kennt SAP verschiedene Verfahren. Es ist ratsam, die Vergangenheitsdaten für die Prognose entsprechend vorzubereiten. Oft wird vernachlässigt, dass diese Verfahren auch für spätere Korrekturen bei der Prognose verwendet werden können. Im Rahmen der Vorbereitungen sollte man auch die Product Lifecycles der verschiedenen Produkte berücksichtigen. So sollte der Ein- und Auslauf neuer bzw. alter Produkte über die Lebenszyklusplanung gesteuert werden. Dazu wird eine Zeitreihe definiert, die den Lebenszyklus abbildet. Danach wird die Prognose mit der Zeitreihe der entsprechenden Periode multipliziert. So wird der Lebenszyklus in die Prognose eingearbeitet.
Eine variierende Anzahl von Arbeitstagen kann bei der Interpretation der Vergangenheitsdaten ebenfalls berücksichtigt werden. Dazu wird im Prognoseprofil die mittlere Anzahl der Arbeitstage hinterlegt (z. B. 20 Tage für einen Monat). Hat ein Monat nun davon eine abweichende Anzahl von Arbeitstagen, so werden die entsprechenden Werte im Verhältnis angepasst. Die Informationen hierzu kommen aus dem Werkskalender, sodass beispielsweise Betriebsferien oder auch Feiertage in Prognosen berücksichtigt werden können.
Oft beeinflussen verkaufsfördernde Maßnahmen (Promotions) Prognosen und Vergangenheitsdaten. Dazu können verschiedene Arten von Promotionen als einmaliges oder regelmäßiges Event (spezielle Feiertage oder Feste wie Weihnachten oder Ostern) angelegt und mit den dazugehörigen Einflüssen hinterlegt werden. So kann sich eine TV-Werbung zu einer 20%-Steigerung bei Produkt A und zu einer 10%-Reduzierung auf Produkt B auswirken. Letztgenannten Fall vergisst man gerne. Er kann jedoch besonders dann auftreten, wenn Produkt A Substitutionsleistungen in Bezug auf Produkt B besitzt. Ausreißer in den Vergangenheitsdaten können ebenfalls die Prognose verfälschen. Dabei handelt es sich bei Ausreißern um Vergangenheitswerte, die nicht in einem erwarteten Wertebereich liegen. Für die Ausreißerkorrektur stehen verschiedene Methoden zur Auswahl:
-
Ausreißerkorrektur mit der Ex-Post-Methode: Grundlage für die Ausreißerkorrektur ist die Ex-Post-Prognose. Dazu werden die Vergangenheitswerte in zwei Gruppen unterteilt. Die erste Gruppe sind die älteren Vergangenheitsdaten. Sie dienen zur Initialisierung der ExPost-Prognose. Die zweite Gruppe enthält die neueren Vergangenheitswerte. Diese dienen zur Durchführung der ExPost-Prognose. Weiterhin wird ein Sigma-Faktor benötigt. Dieser gibt die Toleranz für die Ausreißerkorrektur an. Je kleiner der Sigma-Faktor ist, desto kleiner ist die Toleranz. Somit wird auch eine größere Anzahl von Ausreißern automatisch korrigiert. Anhand der ExPost-Prognose, der mittleren absoluten Abweichung der Ex-Post-Prognose und des Sigma-Faktors wird der Toleranzbereich für die Ausreißerkorrektur ermittelt. Liegt ein Wert außerhalb des Toleranzbereichs, wird der Wert auf den prognostizierten Wert der Ex-Post-Prognose korrigiert. Welches Prognosemodell bei der Ex-Post-Prognose zum Einsatz kommt, hängt vom Prognosemodell ab. Bei einer automatischen Modellauswahl werden die Schritte 2 und 3 durchgeführt, um ein passendes Prognosemodell zu finden.
-
Ausreißerkontrolle mit der Medianmethode: Sie funktioniert ähnlich wie die vorherige Methode. Die Medianmethode sortiert die Werte der Größe nach und nimmt den Wert in der Mitte. Wären z. B. die Vergangenheitsdaten 8, 10, 13, 16, 18, ist der Median 13. Der Median wird für Grund-, Trendwert und Saisonindex ausgerechnet. Anhand dieser Werte kann die Medianmethode für jede Periode einen Erwartungswert ermitteln. Mit dem Erwartungswert und dem Sigma-Faktor kann nun der Toleranzbereich berechnet werden.
2) Test der Vergangenheitsdaten
Über den Test der Vergangenheitsdaten erhält man die entscheidenden Aussagen zur richtigen Wahl der Prognosemethode. Diese basieren auf den aus Schritt 1 korrigierten Vergangenheitsdaten. Dabei darf die Datenbasis der Vergangenheitswerte nicht zu klein gewählt werden. Ab zwei Saisonzyklen oder Berichtszeiträumen kann ein derartiger Test gefahren werden. Die Praxis zeigt jedoch, dass drei bis vier Zyklen beziehungsweise Berichtszeiträume besser wären. Wichtig ist hierbei die Ermittlung unregelmäßiger Bedarfe. Damit sind Nullwerte in den Vergangenheitswerten gemeint. Wären beispielsweise 66% der Vergangenheitswerte Nullwerte, würde dies einen unregelmäßigen Bedarf darstellen.
Wo liegt hier aber die Grenze zwischen regelmäßigem und unregelmäßigem Bedarf? Wäre der entsprechende Grenzwert bei 30 Prozent anzusetzen? Der richtige Wert ist dem entsprechenden Kontext und Betriebsumfeld beim Kunden anzupassen. Definitiv kann hier keine allgemeingültige Maßzahl über alle Unternehmen und Branchen angegeben werden. Fällt der Test auf einen unregelmäßigen Bedarf positiv aus, empfiehlt sich die Croston-Methode einzusetzen. Im nächsten Schritt wird das Streuungsverhalten der Vergangenheitsdaten bewertet. Ist dieses zu stark, so wird das System Schwierigkeiten bei einer akkuraten Prognosemodellauswahl haben und ein Saison- bzw. Trendverlauf kann ausgeschlossen werden. Ansonsten folgt als Nächstes ein kombinierter Saison- und Trendtest. Dabei wird zunächst auf das Saisonverhalten und dann auf das Trendverhalten hin geprüft. Je nachdem, welcher der beiden Tests bessere Werte liefert, erfolgt dann im nächsten Schritt die Modellwahl.
3) Modellselektion
 Aufbauend auf den Tests der Vergangenheitsdaten aus Schritt 2 wird anhand des Testergebnisses eine Modellselektion vorgenommen. Dabei ist eine komplexe Fallunterscheidung zu beachten.
Aufbauend auf den Tests der Vergangenheitsdaten aus Schritt 2 wird anhand des Testergebnisses eine Modellselektion vorgenommen. Dabei ist eine komplexe Fallunterscheidung zu beachten.
Wie bereits erwähnt, liefert die Croston-Methode bei unregelmäßigen Bedarfen die besten Prognose-Ergebnisse. Diese ermittelt die mittlere Bedarfshöhe und die mittlere Dauer zwischen den Nachfragen. Ist beispielsweise die mittlere Bedarfshöhe 10 Stück und die mittlere Dauer 5 Wochen, generieren die Prozesse entlang des Prognosehorizonts alle 5 Wochen einen Bedarf von 10.
Haben die Vergangenheitsdaten eine starke Streuung, ist eine automatische Modellselektion schwierig. Daher wählt hier das System das Konstantmodell mit der exponentiellen Glättung 1. Ordnung aus. Für die Berechnung der Prognose werden die vorgehenden Prognosewerte, die letzten Vergangenheitswerte und der Glättungsfaktor Alpha herangezogen. Ein großer Alpha-Faktor berücksichtigt die Vergangenheit weniger als ein kleiner Alpha-Faktor.
Fällt der Trendtest positiv und der Saisontest negativ aus, so bieten sich nachfolgende Optionen an:
-
Das Konstantmodell mit exponentieller Glättung 1. Ordnung, welche standardmäßig immer berücksichtigt wird.
-
Aufbauend auf der exponentiellen Glättung wird ein Grundwert und ein Trendwert für das Trendmodell berechnet. Daraus leiten sich die Prognosewerte für den Prognosehorizont ab. Hierbei wird ein Glättungsfaktor Alpha für den Grundwert und Glättungsfaktor Beta für den Trendwert herangezogen. Ein großer Alpha-Faktor berücksichtigt den Grundwert weniger als ein kleiner Alpha-Faktor, wobei geringe Beta-Werte stärker den Trend glätten als ein großer Wert.
-
Die lineare Regression kann zur Prognose von Trends verwendet werden. Dabei berücksichtigt diese Methode alle Vergangenheitsdaten und legt eine Gerade mit dem kleinstmöglichen Fehler durch die betreffenden Werte ohne Anwendung einer Glättungsfunktion.
Ist der Saisontest positiv und der Trendtest negativ, werden das Konstantmodell und das Saisonmodell selektiert. Entscheidend sind deshalb in diesem Falle die Glättungsfaktoren Alpha für den Grundwert und Gamma für den Saisonindex. Beta spielt hier keine Rolle, da eine Trend-Komponente in diesem Falle unberücksichtigt bleibt. Ein kleiner Gammawert glättet den Saisonindex stark. Große Gamma-Werte lassen hingegen saisonales Verhalten, beziehungsweise Veränderungen, sehr rasch in die Prognose einfließen.
Sind sowohl Trend- und Saisontest positiv, werden folgende Modelle selektiert:
-
Das Konstantmodell mit exponentieller Glättung 1. Ordnung.
-
Das Trendsaisonmodell als Kombination aus Trend- und Saison-Modell: Es baut auf der exponentiellen Glättung auf, welche somit logischerweise die Glättungsfaktoren Alpha, Beta und Gamma berücksichtigt.
-
Die saisonale lineare Regression berechnet zunächst für jede Periode in der Vergangenheit ein Saisonindex. Diese führt zu einem gemittelten Saisonindex, welcher mit einem Glättungsfaktor geglättet wird. Die Vergangenheitsdaten werden anschließend gemäß der saisonalen Indizes korrigiert und eine lineare Regression durchgeführt. Die berechneten Saisonindizes werden auf die Ergebnisse der linearen Regression angewendet. Dies ergibt dann das Ergebnis der Prognose.
4) Modellauswahl
Nun stellt sich die Frage, welches der ermittelten Modelle am besten geeignet wäre? Die Antwort ist einfach: Das Modell mit dem geringsten Fehlermaß. Je nachdem, ob ein Konstant-, Trend-, Saison- oder Trendsaisonmodell ausgewählt wird, können entsprechend die Faktoren Alpha, Beta und Gamma parametrisiert werden. Hierbei ist einfach strickt die Relation Konstant gleich Alpha, Trend gleich Beta und Saison gleich Gamma anzuwenden. Beim Trend- und Saisonmodell ist dabei stets auch ein Grundwert, also das Konstantmodell zu berücksichtigen.
Das Trendsaisonmodell ist eine Kombination aus Trend- und Saisonmodell, welches in der Konsequenz alle drei Glättungsfaktoren berücksichtigt. Um hier die optimalen Parameter zu finden, testet das System die verschiedenen Kombinationen durch. Dazu muss für jeden Faktor eine Unter-und Obergrenze festgelegt werden (z. B. 0,1 bis 0,5). Daneben benötigt das System noch eine Schrittweite, um die verschiedenen Möglichkeiten zwischen Unter- und Obergrenze durchzutesten. Bei einer Untergrenze von 0,1, einer Obergrenze von 0,7 und einer Schrittweite von 0,1, werden die Kombinationen 0,1, 0,2, 0,3, 0,4, 0,5, 0,6 und 0,7 durchgetestet. Die Schrittweite kann und sollte bei Bedarf angepasst werden, da sie die Ergebnisse bzgl. der Modellauswahl signifikant beeinflusst. Im Standard ist die Schrittweite im Übrigen auf 0,2 eingestellt. Denn für jede Parameter-Kombination der Glättungsfaktoren wird die mittlere absolute Abweichung (MAD) berechnet. Die Kombination mit dem geringsten MAD wird dabei als das Beste zu verwendete Modell angesehen. Darüber hinaus können auch andere Fehlermaße zur Parameterfindung ausgewählt oder gar eigene Verfahren definiert werden.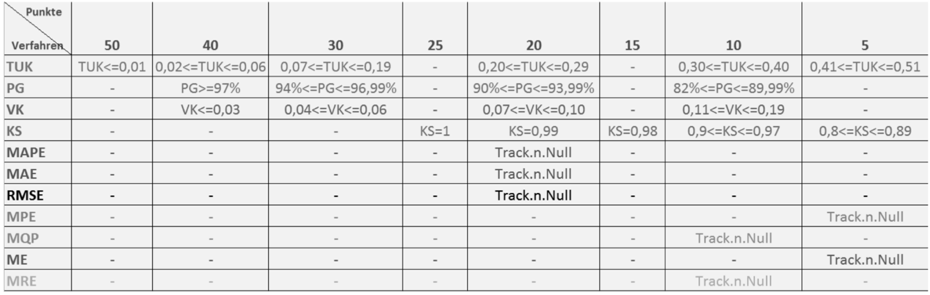
5) Prognose
Anhand des ausgewählten Modells findet nun die Prognose statt. Hierzu wird die Prognose selbst und eine Ex-Post-Prognose durchgeführt. Um nicht bei jedem Prognoselauf die Schritte 2 bis 4 durchführen zu müssen, bietet das System die Möglichkeit, die Prognoseeinstellungen für eine Merkmalskombination abzuspeichern (z. B. Produkt und Lokation). Dies spart Laufzeit.
Bei jedem Prognoselauf ermittelt SAP für jedes untersuchte Produkt auf Basis standardisierter Fehlermaße entsprechende Kennzahlen. Wenn dabei ein bestimmtes Fehlermaß überschritten wird und damit ersichtlich wird, dass die momentanen Prognoseeinstellungen kein gutes Ergebnis mehr hervorbringen, empfehlen sich die Schritte 2 bis 4. Nach einer Prognose können noch weitere Korrekturen notwendig sein (z. B. Arbeitstagekorrektur; vgl. dazu Schritt 1).
6) Kontrolle der Prognosequalität
Im Abschluss der Prognosemaßnahmen sind die Ergebnisse auf deren Genauigkeit zu prüfen. Dazu findet ein Vergleich der Ex-Post-Prognose mit den Vergangenheitsdaten statt. Zum Vergleich stehen unterschiedliche Fehlermaße zur Verfügung.
Standardmäßig werden folgende Fehlermaße (siehe auch Tabelle) unterstützt:
-
Fehlersumme (ET)
-
Mittlere absolute Abweichung (MAD)
-
Mittlerer quadratischer Fehler (MSE)
-
Wurzel des mittleren quadratischen Fehlers (RMSE)
-
Mittlerer absoluter prozentualer Fehler (MAPE)
-
Mittlerer prozentualer Fehler (MPE)
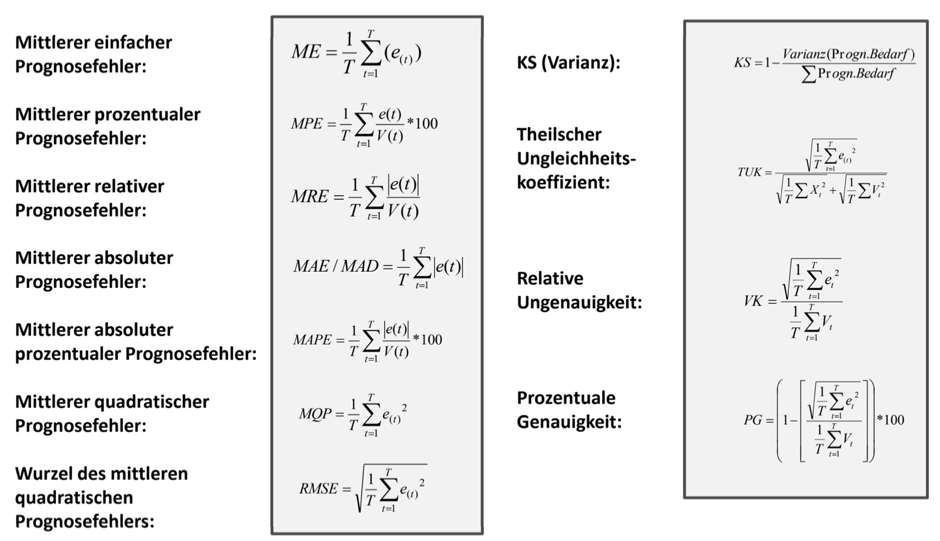
Zusätzlich zu diesen Fehlermaßen können auch eigene Fehlermaße definiert werden. Um nicht alle Prognoseergebnisse im Detail begutachten zu müssen, empfiehlt sich die Nutzung der Prognoseprotokollierung. Dabei können die Systeme Ausnahmemeldungen, sogenannte Alerts, erzeugen. Durch Anpassung der Grenzwerte in den Prognoseprofilen kann gesteuert werden, wann die Alerts ausgelöst werden.
Die Konfiguration kann dabei festlegen, wann eine Informationsmeldung, Warnmeldung oder Fehlermeldung auszugeben ist. Anhand der Meldungen muss der Sachbearbeiter nun die Prognose korrigieren (Prognoseeinstellungen oder Vergangenheitsdaten). Dazu kann er beispielsweise eine interaktive Prognose durchführen und eine manuelle Auswahl der Prognosemethode vornehmen.
Fazit
Die Etablierung einer Prognose innerhalb von SAP MM oder SAP APO kann den Einkauf im Rahmen des Einkaufsmanagements von vielen Routinearbeiten entlasten, wenn diese auf den konkreten Kontext und die unternehmensspezifischen Anforderungen beziehungsweise Bedürfnisse angepasst sind. Hierbei helfen die SAP Standardmodelle in vielen Fällen.
In Bezug auf die Ausnahmen ist es entscheidend, dass hierzu in beiden Systemen eigene Routinen und Verfahren etabliert werden können. Wichtig ist auch eine umfassende Vorbereitung im Rahmen der Einführung von Prognoseprozessen. Es gibt zwar viele Fehlerkenngrößen in SAP, deren Bedeutung aber oft unterschätzt oder deren Werte nicht beachtet werden. In der Folge können sich Prognosefehler kumulieren, sodass die Aussagekraft der Prognosen gering ist.
Es empfiehlt sich deshalb, professionelle Beratung im Rahmen dieser Maßnahmen zu berücksichtigen, damit sich ein ROI möglichst rasch realisieren lässt.





